회사에서 기술 세미나를 준비하면서 아주 세세하게, 기존의 논문 리뷰와 다른 형식으로 논문 리뷰 글을 작성해보았습니다.
해당 논문은 요즘 주목받고 있는 OpenAI의 o1, o3, Deepseek의 r1과 같이 추론 모델의 근간이 된 Test-Time Scaling을 LLM에서 실험해본 논문으로, 개인적으로 "모델이 더 오래 생각한다니.."하고 흥미롭게 읽었습니다.
게다가 젠슨 황이 pre-training, post-training을 이은 Scaling Laws의 새로운 단계는 Test-Time Scaling이라고 언급한 것을 보았는데, 그것 덕분에 Test-Time Scaling이 추론 모델에 얼마나 큰 반향을 불러일으킬지에 집중하면서 읽을 수 있었습니다.
Background
먼저 논문에 등장하는 test time scaling이 무엇인지, 어떤 이유로 최근에 주목받고 있는지 알아보도록 하겠습니다.
Train-Time Scaling vs Test-Time Scaling
LLM의 성능을 향상시키는 방법에는 어떤 것이 있을까요?
지금까지 우리는 대부분 모델을 학습하는 것에 포커스를 맞춰서 성능 향상을 생각해왔습니다.
더 많은 데이터, 더 큰 모델, 더 오래 학습을 하는 것이 더 좋은 모델을 만들기 위한 길이라고 여겨왔었는데요.
- 이렇게 학습 과정에서 데이터셋 사이즈, 모델 파라미터 수, 연산량을 증가시켜 성능을 확장시키는 방법을 “Train-Time Scaling”이라고 합니다.
- 또 데이터셋 사이즈, 모델 파라미터 수, 연산량 총 세 개를 AI의 화석연료, “Train-time compute”라고 합니다.

실제로 자원과 연산량을 늘릴수록 모델의 성능이 좋아지기는 하였으나, Train-Time Scaling에는 분명한 한계가 존재합니다.
- 일단 이렇게 학습에 자원을 많이 투자하는 것은 돈이 많이 드는 일입니다.
모델이 잘못된 대답을 내놓아도 모델의 출력이 한 번에 이루어지기 때문에 추론 과정 중 수정할 수 없으며, 잘못된 대답을 바로 잡으려면 튜닝된 데이터로 모델을 다시 학습해야 하는 방법밖에 없습니다. 이렇게 되면 또 돈과 시간이 쓰이게 됩니다. - Train-time compute를 늘릴수록 성능이 향상되는 것은 맞으나, 그 향상폭이 점점 줄어들고 있습니다.
따라서 원하는 성능을 얻기 위해서는 학습 비용이 기하급수적으로 늘어나게 됩니다.
여기서 의문이 제기됩니다. “어? 우리가 벽에 도달한건가?”
이런 배경에서 등장한 것이 Test-Time Scaling입니다.
”Test-Time Scaling”은 학습 과정에서 추가적인 컴퓨팅 자원을 투입하는 Train-Time Scaling과 달리 추론 과정
에서 컴퓨팅 자원을 활용하여 성능을 개선하는 방법입니다.

“사람이 어려운 문제에 직면했을 때 더 많은 시간을 들려 신중하게 생각함으로써 더 나은 결정을 내리듯이,
모델도 추론 과정 즉 테스트 시점에서 추가적인 연산 자원을 활용하여 문제 해결 능력을 향상시킬 수 없을까?” 라는 아이디어에서 착안되었습니다.
대표적인 사례로 OpenAI의 o1 모델이 언급되고는 합니다.
o1 모델은 빠른 직관적 사고 대신 느린 이성적 사고를 도입하여, 질문이 복잡할수록 추론 단계를 늘려 더 깊이 생각하도록 설계된 모델입니다. 이 말인 즉슨 질문이 복잡할수록 테스트 시점의 연산을 추가하여 답변의 논리성과 정확성을 향상시킨 것으로 Test-Time Scaling을 사용한 사례라고 할 수 있다는 것입니다.
Introduction
이러한 Test-Time Scaling을 효율적으로 활용할 수 있는 방법을 본 논문에서는 제시하고 있는데요!
같이 논문 내용을 살펴보겠습니다.
연구 배경은 다음과 같습니다.
- 저자들은 Test-Time Scaling의 중요성을 자가 개선하는 에이전트를 들며 설명하였습니다. 자가 개선 에이전트는 단순히 주어진 작업을 수행하는 것을 넘어, 자신의 행동을 분석하고 학습하여 미래에 더 나은 결과를 얻도록 개선하는 에이전트인데요. 자가 개선 에이전트가 되기 위해서는 모델이 지속적으로 학습하고 개선되어야 하는데, Test-Time Scaling은 개선을 가능하게 하는 중요한 도구로 Test-Time Scaling에 대한 연구가 제대로 이루어져야 함을 주장하였습니다.
- Test-Time Scaling이 이렇게 중요하게 활용될 수 있음에도 이전의 선행 연구들은 Test-Time Scaling에 대해 제대로 연구하지 못하였었습니다. 어떤 연구에서는 Test-Time Scaling이 효과적이라는 긍정적인 의견이, 어떤 연구에서는 효과적이지 않다는 부정적인 의견이 나오면서 엇갈린 결과를 보이기도 하였는데요. 따라서 본 논문에서는 Test-Time Scaling에 대한 다양한 접근 방식을 체계적으로 분석하였습니다.
본 논문의 전체 내용을 관통하는 핵심 질문은 다음과 같습니다.
“고정된 연산 자원 안에서 LLM이 복잡한 프롬프트에 대해 얼마나 성능을 향상시킬 수 있을까?”
논문은 다음과 같은 기여를 하며, 핵심 질문에 대한 해답을 탐구하였습니다.
- 첫번째로 프롬프트의 난이도에 따라 최적의 Test-Time Scaling 전략이 달라진다는 점을 강조하며, 난이도에 따라 테스트 시점 연산 자원을 효과적으로 할당할 수 있는 “compute-optimal” 스케일링 전략을 제안하였습니다.
- 또한 순전히 Train-Time Scaling에 집중하기보다는, 프롬프트의 난이도에 따라서 적은 컴퓨팅 자원으로 작은 모델을 사전 학습하고 Test-Time Scaling을 적용하여 모델의 사고 과정을 개선하는 것이 더 효과적일 수 있음을 보여줬습니다.
Test-Time Scaling Strategies: Searching and Modifying
난이도에 따라 테스트 시점 연산 전략을 어떻게 효율적으로 배치하는지를 알아보기 전에 Test-Time Scaling 전략에는 어떤 것이 있는지 알아보도록 하겠습니다.
Test-Time Scaling 전략은 크게 두 가지가 있습니다.

왼쪽은 프로세스 기반 보상 모델(검증자)을 활용한 탐색 기법으로,
- 여러 개의 다양한 답변을 생성한 후,
- 프로세스 기반 보상 모델을 활용하여 가장 높은 점수를 받은 답변을 선택하는 방식입니다.
오른쪽은 프롬프트를 고려하여 답변 분포를 적응적으로 업데이트하는 기법입니다.
- 모델이 반복적으로 자신의 답변을 수정해나가면서 여러 개의 답변을 순차적으로 생성하고,
- 생성된 답변들 가운데 프로세스 기반 보상 모델로 가장 높은 점수를 받은 답변을 선택하는 방식입니다.
모델이 스스로 답변을 수정하는 것을 base LLM이 제안한 답변 분포를 업데이트한다고 말하는 것입니다.
여기서 특이한 점은 결과 기반 보상 모델(Outcome-based Reward Model, 즉 ORM)이 아닌 프로세스 기반 보상 모델(Process-based Reward Model, 즉 PRM)을 사용한다는 점입니다.
결과 기반 보상 모델은 무엇이고 또 프로세스 기반 보상 모델은 무엇일까요?
LLM이 사람의 피드백을 반영하며 학습을 하기 위해서는, 생성한 답변이 좋은 답변인지 나쁜 답변인지를 구별할 수 있어야 하는데, 이 때 사용하는 것이 보상 모델입니다.
결과 기반 보상 모델은 일반적인 보상 모델로 출력된 답변만 보고 점수를 부여합니다. 이와 달리 프로세스 기반 보상 모델은 답변이 추론되는 과정까지 평가하여 점수를 부여합니다.
예를 들어, “2x3+4는 얼마인가요?”라는 질문에
- 답변 1: “2x3=5, 5+4=9, 답은 10”,
- 답변 2: “2x3=6, 6+4=10, 답은 10” 라는 두 개의 답변이 출력되었다면,
결과 기반 보상 모델은 두 개의 답변 모두 정답을 출력했으므로 두 답변 모두에게 높은 점수를 부여하겠지만,프로세스 기반 보상 모델은 답변이 유도되는 과정이 논리적인지까지 평가하여 답변 1의 논리적이지 못한 추론 과정을 감점하여 답변 2에 더 높은 점수를 부여할 것입니다.
따라서 프로세스 기반 보상 모델을 통해 여러 개의 다양한 답변의 추론 과정을 단계별로 평가함으로써 좀 더 논리적인 답변을 선택할 수 있습니다.
How to Scale Test-Time Computation Optimally
이제 본론인 compute-optimal 스케일링 전략에 대해 설명하도록 하겠습니다.
compute-optimal 스케일링 전략은 주어진 프롬프트에 대해서 최대의 퍼포먼스를 낼 수 있는 Test-Time Compute Scaling 전략을 선택하겠다는 전략입니다.
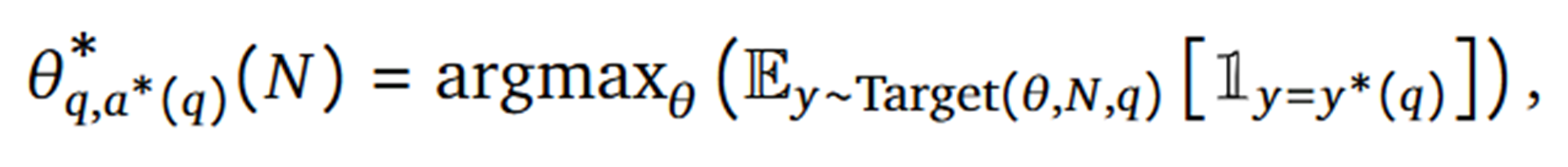
이와 같이 전략이 수식으로도 표현이 되어있는데요. 주어진 프롬프트 q에 대해, 고정된 연산 예산 N 내에서 모델이 정답을 생성할 확률을 가장 높이는 Test-Time Scaling 전략을 찾는 과정을 수식화한 것입니다. (사실 수식을 이해하지 않아도 논문 내용을 이해하는 데에는 아무 문제 없습니다.)
조금 더 자세하게 설명하자면,
- 주어진 프롬프트 q, 연산 예산 N, 전략 theta에 따라 모델이 생성하는 분포 Target에서 출력 y를 샘플링
- 샘플링한 출력 y가 ground-truth y*와 일치할 확률의 기댓값을 구하고,
- 그 기댓값이 가장 큰 전략 theta를 프롬프트 q, 연산 예산 N에 따른 최적의 전략이라고 판단하게 됩니다.
근데 이제 핵심 질문(“고정된 연산 자원 안에서 LLM이 복잡한 프롬프트에 대해 얼마나 성능을 향상시킬 수 있을까?”)으로 되돌아 가보자면 연산 예산 N은 고정되어 있으므로 우리는 프롬프트에 따라, 특히 프롬프트의 난이도에 따라 최적의 Test-Time Scaling 전략을 고르면 됩니다.
그러면 이제 프롬프트의 난이도는 어떻게 측정할 수 있을지 의문이 생기실 것입니다.
프롬프트의 난이도를 측정하는 방법에는 두 가지가 있습니다.
- Oracle Difficulty: 모델의 pass@1 rate(모델이 처음 출력한 답변이 정답일 확률)을 기준으로 pass@1 rate가 높을수록 쉽다고 판단하는 방법입니다. ground-truth에 접근 가능해야 실행할 수 있습니다.
- Model-Predicted Difficulty: 실제 배포 환경에서는 ground-truth를 알 수 없으므로, 학습된 검증자(보상 모델)의 평균 최종 답변 점수를 사용하여 난이도를 추정합니다. 검증자를 통해 프롬프트의 난이도를 추정하는 것은 추가적인 계산 비용을 발생시킵니다.
이렇게 프롬프트에 따른 확률 또는 점수를 매긴 후, 그 값에 따라 5개의 난이도 구간(레벨)으로 프롬프트들을 나눕니다. 이 때 레벨 1은 ‘가장 쉬움’, 레벨 5는 ‘가장 어려움’을 나타냅니다.
실험 전에 검증 세트에 대해서 확률 또는 점수를 매겨 난이도 구간을 설정해놓고, 나머지 테스트 세트에 대해서 난이도 레벨을 매겼습니다.
Experiments
본 논문에서는 프롬프트(문제)의 난이도에 따라 어떠한 Test-Time Scaling 전략이 적합한 지를 실험해보고자 하였습니다.
- 먼저 여러 개의 답변을 생성하고 그 답변들을 탐색하는 전략에는 다양한 방식이 있는데 이러한 방식들의 난이도에 따른 성능 변화에 대해 알아보고,
- 여러 개의 다양한 답변을 병렬로 샘플링하는 방식(프로세스 기반 보상 모델(검증자)을 활용한 탐색 기법)과 순차적으로 답변을 샘플링하며 수정해나가는 방식(프롬프트를 고려하여 답변 분포를 적응적으로 업데이트하는 기법)의 난이도에 따른 성능 변화에 대해 알아볼 것입니다.
- 또한 고정된 연산 예산 내에서 문제의 난이도에 따라 추가적인 사전 학습이 더 효과적인지, 추가적인 테스트 시점 연산이 더 효과적인지도 확인해보는 시간을 갖고자 합니다.
실험 세팅은 다음과 같습니다.
- Model: PaLM 2-S base model (closed model)
- Dataset: MATH benchmark
|
problem
|
How many positive whole-number divisors does 196 have? |
| solution | First prime factorize $196=2^2\cdot7^2$. The prime factorization of any divisor of 196 cannot include any primes other than 2 and 7. We are free to choose either 0, 1, or 2 as the exponent of 2 in the prime factorization of a divisor of 196. Similarly, we may choose 0, 1, or 2 as the exponent of 7. In total, there are $3\times 3=9$ possibilities for the prime factorization of a divisor of 196. Distinct prime factorizations correspond to distinct integers, so there are $\boxed{9}$ divisors of 196. |
| answer | 9 |
| subject | Number Theory |
| level | 3 |
Experiment 1: Test-Time Scaling for Search with Verifiers
여러 개의 답변을 생성하고 그 답변들을 탐색하는 전략에는 다양한 방식이 있습니다.

- Best-of-N weighted: 베이스 LLM에서 N개의 답변을 얻은 후 프로세스 기반 보상 모델로부터 얻은 점수에 따라 최종 답변을 선택합니다.
- Beam Search: 프로세스 기반 보상 모델을 사용해서 사고 과정 내 단계별 예측을 최적화하는 탐색 알고리즘입니다.
- 이 알고리즘에는 빔의 개수 N과 빔의 너비 M이라는 하이퍼 파라미터가 존재합니다. 이렇게 빔의 개수, 너비를 제한함으로써 답변 공간을 모두 탐색하는 것보다 가장 유망한 후보들을 따라 탐색하게 됩니다. 따라서 전체 탐색 공간을 줄여 효율성을 높일 수 있습니다.
- 단계는 다음과 같습니다.
1. 높은 Temperature를 설정하여 다양하게 N개의 초기 예측을 수행합니다.
2. 프로세스 기반 보상 모델을 사용해서 각 예측의 reward-to-go 값(예측 보상값)을 예측하고, 이를 기반으로 각 예측을 평가합니다.
3. 상위 N/M 개의 답변만 후보로 남깁니다.
4. 선택된 각 후보당 M개의 새로운 답변을 생성하도록 하여 총 N/M * M개의 후보가 있도록 합니다.
5. 완료되거나 최대 빔 확장 횟수에 도달할 때까지 2~4 단계를 반복합니다.
- Lookahead Search: 빔 서치의 각 단계에서 프로세스 기반 보상 모델의 현재 점수 대신 k단계만큼 미래의 보상 모델 점수를 활용해 후보를 평가하는 방법입니다.
- 기존의 빔 서치에서 각 단계의 reward-to-go 값을 예측할 때 k단계만큼 롤아웃(뒤의 단계 시뮬레이션)하여 예측한다는 점만 다릅니다. 이렇게 롤아웃 시뮬레이션을 할 때는 분산을 최소화하기 위해 Temperature를 0으로 두어 가장 가능성 높은 경로만 따라가도록 합니다.
- 기존 빔 서치보다 각 단계에 대한 가치 추정 점수 정확도를 향상시킬 수 있지만, 시뮬레이션하는 부분에서 추가적인 계산 비용이 발생합니다.
Analysis Results 1: Test-Time Scaling for Search with Verifiers
연산 예산에 따라, 프롬프트의 난이도에 따라 세 가지 전략을 분석한 결과는 다음과 같습니다.

- 연산 예산과 문제의 난이도에 따라 최적의 검증자 기반 탐색 방식은 다릅니다.
- 빔 서치는 문제가 어려울 때, 연산 예산(추론 토큰 수)이 적을 때 더 효과적입니다.
- 왼쪽 그래프를 보시면, 연산 예산이 적을 때는 빔 서치가 우수하나 예산이 많아질수록 성능 향상 폭이 줄어들고 best-of-N보다 못한 결과를 보이기도 함을 확인할 수 있습니다.
- 아래의 예시와 같이, 빔 서치에서 필요한 예산보다 더 많은 예산이 주어지면 검색 과정에서 알맹이 없는 반복적인 스텝을 생성하는 경우가 발생합니다.
- 오른쪽 그래프를 보시면, 레벨 4,5의 어려운 문제들에서 빔 서치의 정확도가 다른 방식들에 비해 월등한 성능을 보이고 있음을 확인하실 수 있습니다. 직관적으로 생각해봐도 어려운 문제의 경우 쉬운 문제에 비해 초기 답변의 품질이 떨어지기 때문에 올바른 답변으로 유도하는 탐색 알고리즘이 필요할 것입니다. 따라서 단순히 좋은 출력을 우연히 얻는 것(Best-of-N)보다 점진적으로 최적의 출력을 찾아가는 beam search 방식이 유리할 것입니다.

- best-of-N은 문제가 쉬울 때, 연산 예산이 높을 때 더 효과적입니다.
- 왼쪽 그래프를 보시면, 생성 예산이 늘어남에 따라 best-of-N이 빔 서치의 성능을 능가한 것을 보실 수 있습니다. 더 많은 경우의 수를 생성할수록, 좋은 답변을 선택할 확률이 올라가기 때문입니다.
- 오른쪽 그래프를 보시면, 문제가 쉬운 경우에는 best-of-N도 효과적인 방법으로 작용하는데, 쉬운 문제에서는 base LLM에서 충분히 좋은 품질의 출력을 얻을 수 있기 때문에 굳이 깊이 있는 탐색을 하지 않아도 되기 때문입니다.

- 논문 저자들의 주장처럼 프롬프트의 난이도를 결정하는 것이 최적의 Test-Time Compute Scaling 전략을 결정하는 데에 효과적인 지표라는 사실을 확인할 수 있습니다.
- 문제의 난이도, 주어진 연산 예산에 따라 최적의 탐색 방식을 선택하는 것이 단순 best-of-N을 사용하는 것보다 동일 성능 대비 4배 연산을 아낄 수 있습니다. (16 vs 64)
Experiment 2: Test-Time Scaling for Revisions
다음으로는 revision model을 통해 모델이 반복적으로 답변을 개선해나가는 방법에 대한 실험 방법 및 그 결과 분석에 대해 설명하겠습니다.
먼저 실험을 어떻게 진행하였는지에 대해서 설명하겠습니다.
본 논문의 저자들은 기존의 LLM에 프롬프트를 다르게 입력하는 것만으로 모델이 자신의 답변(사고 과정)을 자체적으로 개선하게 할 수는 없다고 생각하였고, 모델이 스스로 자신의 답변을 반복적으로 개선할 수 있도록 파인튜닝을 시도하였습니다. 이 파인튜닝한 모델을 revision model이라고 부릅니다.

파인튜닝 과정에 대해 간단하게 설명하자면, 저자들은 revision dataset을 구축하였습니다.
오답 시퀀스 뒤에 정답 시퀀스가 배치되도록 결합하여 학습 데이터를 구축하여 모델이 아예 새로 답변을 생성하는 것이 아니라 맥락 속에서 실수를 인식하고 수정하는 능력을 갖도록 하였습니다.
하지만 파인튜닝한 revision model을 단독으로 사용할 수는 없었습니다. 수정 과정을 거친 38%의 올바른 답변들이 다시 올바르지 않은 답변으로 수정되는 경향이 있었기 때문입니다. 따라서 본 논문에서는 revision model의 출력들에 majority voting 또는 verifier based selection을 적용하여 여러 출력들 중 가장 적합한 것을 고르도록 하였습니다.

논문 실험에 사용됐던 revision model의 성능에 대한 그래프입니다.

왼쪽 그래프를 보시면, y축이 증가할수록 모델이 한 응답에 대한 수정 스텝을 많이 거친, 샘플링한 샘플링이 길다고 보실 수 있습니다. 체인이 더 길 수록 pass@1 스코어가 향상되는 것으로 보아 모델이 이전 답변의 실수를 식별하고 수정하는 능력을 성공적으로 학습했음을 알 수 있습니다.
오른쪽 그래프를 보시면, 병렬적으로 샘플링 한 후 majority voting 이나 verifier based selection으로 답변을 선택하는 것보다 순차적으로 답변을 수정해나가며 여러 답변을 생성하고 그 답변 안에서 최고의 답변을 고르는 방식이 더 우수함을 알 수 있습니다.
Analysis Results 2: Test-Time Scaling for Revisions
revision model을 마련했다면 이제 문제의 난이도에 따른 병렬 탐색 방식과 순차 개선 방식을 비교해볼 차례입니다. 간단하게 병렬 탐색 방식, 순차 개선 방식이라는 용어로 표현하였는데
- 병렬 탐색 방식은 앞에서 설명하였던 병렬로 여러 답변들을 생성한 후 탐색하는 방식들을 말합니다. 문제를 해결하기 위한 다양한 접근 방식들을 모두 탐색할 수 있어 넓은 글로벌한 탐색을 수행합니다. (e.g. best-of-N, beam search)
- 순차 개선 방식도 앞에서 설명하였듯이 올바른 방향으로 어느 정도 향해있는 답변을 좀 더 올바르게 수정함으로써 지역적으로 정제하는 프로세스를 수행한다고 보시면 됩니다.

- 왼쪽 그래프를 보시면, 고정된 연산 예산(number of generations) 내 최고의 정확도를 달성하는 이상적인 순차 개선 방식- 병렬 탐색 방식 의 비율이 존재함을 알 수 있습니다.
- 이와 마찬가지로 오른쪽 그래프 속에서도 문제의 난이도에 따라 최고의 정확도를 달성하는 이상적인 순차 개선 방식- 병렬 탐색 방식 비율이 존재함을 알 수 있습니다.
- 오른쪽 그래프를 더 자세히 보시면, 쉬운 문제일수록 순차적으로 수정하는 전략이 유리하고어려운 문제일수록 두 방식 사이의 이상적인 비율에서 유리한 것을 볼 수 있습니다.
병렬 탐색 방식 과 순차 개선 방식의 특징을 생각해보았을 때,- 쉬운 문제일수록 초기 답변이 이미 충분히 훌륭하기 때문에 조금만 수정해주면 최적의 답변을 만들 수 있다는 점에서 순차 개선 방식이 유리하고
- 어려운 문제일수록 초기 답변의 방향이 이미 틀렸기 때문에 최대한 다양한 답변들을 생성한 후 보다 올바른 방향의 답변을 선택하는 것인 병렬 탐색 방식과 순차 개선 방식의 혼합이 유리합니다.

- 이 그래프는 문제의 난이도에 따라 최적의 Test-Time Scaling 전략을 적용하는 compute optimal 전략과 단순 병렬 샘플링을 비교하는 그래프입니다.
- 문제 난이도, 테스트 시점 연산 예산에 따라 이상적인 방식을 선택하는 것이 단순한 병렬 best-of-N 샘플링보다 동일 성능 대비 4배 더 적은 연산량을 사용하는 것을 확인하실 수 있습니다. (64 vs 256)
Analysis Results 3: Exchanging Pretraining and Test-Time Compute

이 그래프는 FLOPs를 일치시킨 상태 (= 특정 모델의 Train-Time Compute와 Test-Time Compute의 총 합이 동일한 수준에서 비교할 수 있도록 설정) 에서 소규모 모델+Test-Time Scaling vs 대규모 모델 비교한 그래프입니다.
이 그래프에서 확인할 수 있는 점을 다음과 같습니다.
- 테스트 시점 연산과 사전 학습 연산은 1대1 매치가 되지 않는 것을 볼 수 있습니다.
x(x축의 x)가 증가함에 따라서 추론 과정에 사용되는 연산량 증가
→ 고정된 연산 자원 내에서 할당하는 것(FLOPs 일치)이기에 사전학습 연산량 감소
→ 그래도 성능 우상향
⇒ Test-Time Scaling이 Train-Time Scaling보다 동일 연산 대비 더 큰 효과를 가져다 줌
- 쉬운, 보통의 난이도의 문제의 경우, 별이 선보다 밑에 위치한 경우가 많은 것을 보아 Test-Time Scaling이 Train-Time Scaling(사전학습)보다 효과적임을 알 수 있습니다. 이것은 모델 자체의 능력으로 충분히 좋은 답변을 만들 수 있는 쉬운 문제의 경우, 추가적인 사전 학습없이 테스트 시점 연산만으로 모델 자체 추론 능력을 충분히 끌어올 수 있음을 의미합니다.
- 어려운 문제의 경우, 별이 선보다 위에 위치해 있는 것을 보아 Train-Time Scaling(사전학습)이 Test-Time Scaling보다 효과적임을 알 수 있습니다. 이것은 어려운 문제는 베이스 모델의 능력 밖의 능력을 요구할 수 있어 사전 학습을 통해 모델의 성능을 높이는 것이 더 효과적일 수 있음을 의미합니다.
여기서 Test-Time Scaling의 한계를 알 수 있습니다.
Test-Time Scaling이 모델이 가지고 있는 능력을 최대한 활용할 수 있도록 끌어오는 것이지, 모델의 능력을 새롭게 확장시키는 기술은 아니라는 말입니다. 따라서 모델이 가지고 있는 지식이 적은 상태라면 Test-Time Scaling은 유효하지 않습니다. 예를 들자면 초등학생이 오래 생각한다고 해서 고등학교 교육과정 문제는 풀지 못합니다.
Conclusion
본 논문의 결론을 정리해보자면, 다음과 같습니다.

- 문제의 난이도, 주어진 연산 예산에 따라 최적의 Test-Time Scaling 전략을 선택하는 것이 단순 Best-of-N을 사용하는 것보다 동일 성능 대비 약 4배의 연산 절약 가능합니다.
- 문제가 쉬울 경우에는 순차적으로 답변을 개선하는 방법이, 어려울 경우에는 병렬적으로 답변 생성 후 탐색하는 방법 (특히 Beam Search)과 혼합해서 사용하는 것이 유리합니다.
- 어려운 문제에서는 사전 학습이 더 효과적이나, 쉬운 문제와 같은 특정 상황에서는 Test-Time Scaling이 사전 학습을 대체할 수 있습니다.
Future Works
-
어려운 문제에서도 Train-Time Scaling의 성능을 능가할 수 있는 새로운 Test-Time Scaling 전략을 개발해야 함(Test-Time Scaling의 한계 극복)

- 프롬프트(질문)의 난이도를 보다 효율적으로 추정하는 방법(프롬프트 난이도 예측용 모델 파인튜닝) 연구 필요
- Test-Time Scaling과 Train-Time Scaling을 결합하여 LLM 자체를 개선하는 반복적인 self-improvement 루프 구축
해당 논문과 관련된 발표자료가 필요하시다면 비밀 댓글 부탁드립니다!
그리고 혹시 읽으시고 의문이 드는 부분이 있다거나 함께 나누고픈 생각이 있으시다면 댓글 부탁드립니다.
Reference
- https://huggingface.co/spaces/HuggingFaceH4/blogpost-scaling-test-time-compute
- https://huggingface.co/learn/cookbook/search_and_learn#4-continuing-the-journey-and-resources-
- https://devocean.sk.com/experts/techBoardDetail.do?ID=167287&boardType=experts&page=&searchData=&subIndex=&idList=&searchText=&techType=&searchDataSub=&searchDataMain=&writerID=automan&comment=
- https://newsletter.maartengrootendorst.com/p/a-visual-guide-to-reasoning-llms
- https://discuss.pytorch.kr/t/deep-research-test-time-compute-test-time-scaling/6153
- https://github.com/huggingface/search-and-learn